Музеи и архивы
Первая модель прибора для сложения и вычитания хранится в Музее истории Санкт-Петербурга (выставлена в Комендантском доме Петропавловской крепости).
Оригинальные статьи П. Л. Чебышева
Счётная машина с непрерывным движением / По кн.: Полное собрание сочинений П. Л. Чебышева. Том IV. Теория механизмов. — М.—Л.: Изд-во АН СССР. 1948. С. 158–160.
Исследования
В. Г. Бооль. Арифмометр Чебышева // Известия Императорского общества любителей естествознания, антропологии и этнографии, состоящего при Императорском Московском университете. Т. XCI, вып. 1. Труды Отделения физических наук общества любителей естествознания. 1894. Т. 7, вып. 1. С. 12–22.
В. Г. Бооль. Арифмометр Чебышева // Вестник опытной физики и элементарной математики. 1895. Семестр XVIII. № 205, с. 5-10; № 207, с. 52–56; № 210, с. 134–141.
И. И. Артоболевский, Н. И. Левитский. Механизмы П. Л. Чебышева / В кн.: Научное наследие П. Л. Чебышева. Вып. II. Теория механизмов. — М.—Л.: Изд-во АН СССР. 1945. С. 236.
И. И. Артоболевский, Н. И. Левитский. Модели механизмов П. Л. Чебышева / В кн.: Полное собрание сочинений П. Л. Чебышева. Том IV. Теория механизмов. — М.—Л.: Изд-во АН СССР. 1948. С. 242.
Другие материалы
Арифмометр. Вторая модель с множительной приставкой.
Инвентарная книга Кабинета практической механики Санкт-Петербургского университета (1865—1928).
Письмо П. Л. Чебышеву от В. фон Бооля о написании им статьи о второй модели арифмометра (Архив РАН, фонд 505, опись 1, № 56).
Описание
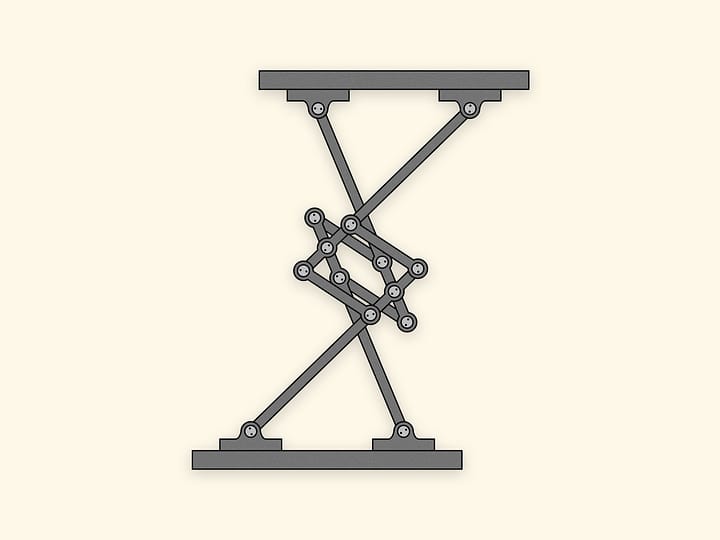
Во времена Пафнутия Львовича Чебышева счётные машины с прерывным изменением цифр обладали ещё значительными конструктивными недостатками (арифмометр Однера появился позднее), и это побудило Чебышева к созданию арифмометра непрерывного действия. Если в машинах с прерывным изменением цифр суммы колесо высшего разряда продвигается сразу на одно деление, когда колесо низшего разряда переходит с 9 на 0, то при непрерывной передаче колесо высшего разряда постепенно поворачивается на одно деление, пока младшее совершает полный оборот.
Было изготовлено две модели арифмометра, выполняющего сложения и вычитания. Первая хранится в Музее истории Санкт-Петербурга (в 2010 году экспонировалась в комендантском доме Петропавловской крепости), вторая, доработанная, хранится в Musée des arts et métiers du Conservatoire national des arts et métiers (Париж, Франция). Ко второй модели уже после её создания Чебышев конструирует дополнительный механизм, позволяющий выполнять умножение и деление.
Арифмометр Чебышева не получил широкого распространения, т.к. учёный имел в виду продемонстрировать принцип работы, а не создать удобный к использованию аппарат. После изобретения колеса Однера появились великолепные арифмометры, известные многим жившим в СССР под названием «Феликс». Однако при переходе к электрическим счётным устройствам и, соответственно, увеличении скорости счёта прерывистое движение влекло сильные толчки. на этом этапе, в середине XX века, и понадобились идеи, которые заложил Пафнутий Львович в свой арифмометр почти за век до этого.
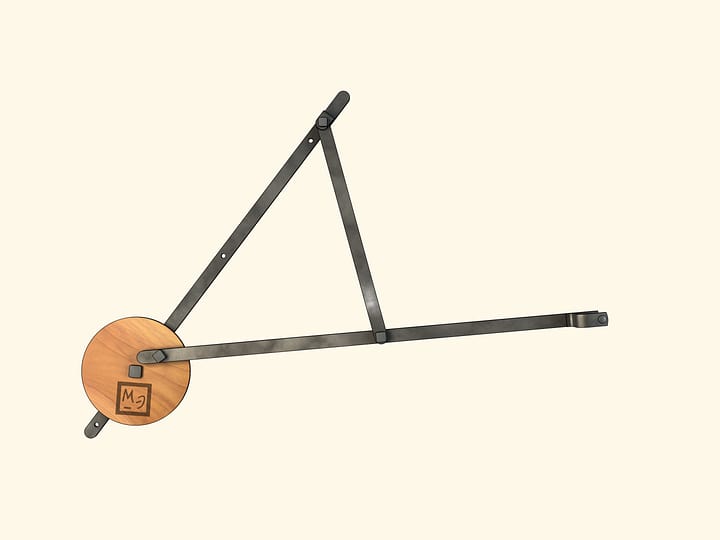
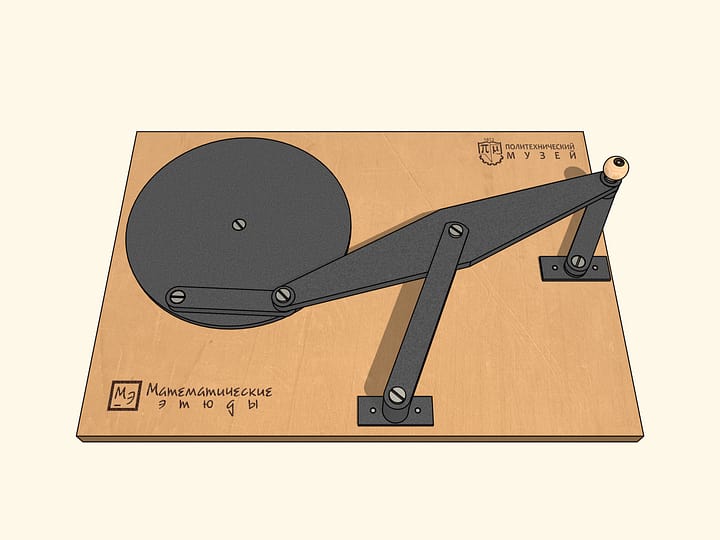
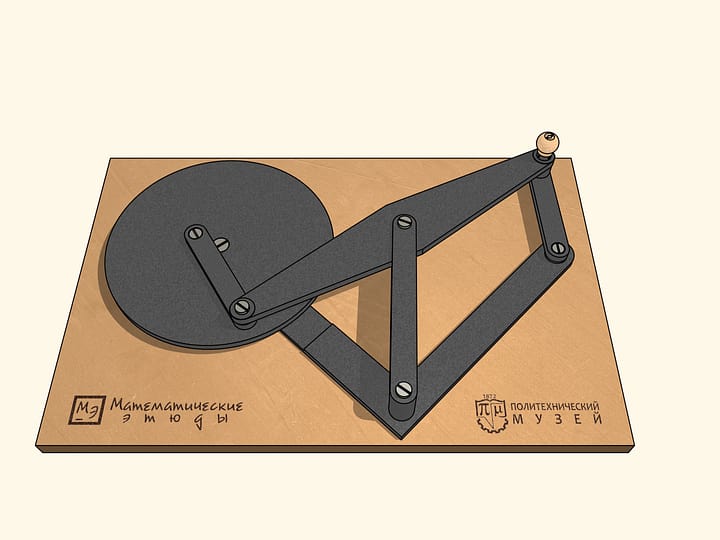
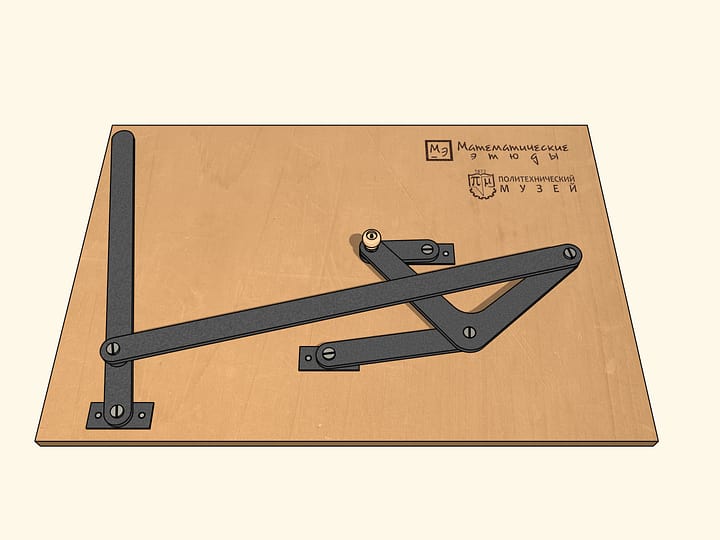
Устройство арифмометра основано на планетарной передаче. При движении любого барабана на одно деление цифровой круг этого же разряда поворачивается на единицу. При этом все более правые цифровые круги остаются на месте. Цифровой круг разряда, расположенного левее поворачиваемого, смещается на 1/10, следующий слева круг — на 1/100 и так далее. Хорошее описание парижского арифмометра и его принципа работы дано в статье В.Г. Бооля.
Фильм демонстрирует первую модель арифмометра и способ работы с ним.
Проведём сложение 415 с 97. Для начала отложим число 415. Чтобы отложить пятёрку в разряде единиц, надо на соответствующем зубчатом колесе взяться за планку ниже пятёрки на неподвижной шкале и опустить её максимально возможно вниз. Так же поступают и для откладывания единицы и четвёрки в соответствующих разрядах. Чтобы к этому числу прибавить второе слагаемое, на уже существующей конфигурации цифровых барабанов нужно отложить число семь в разряде единиц и девять — в разряде десятков. Результат получен. Осталось его считать.
Чебышев пишет про вторую модель:
…непрерывными измѣненiями ихъ показанiй. Но такъ какъ при этомъ чтенiе цыфръ становится болѣе труднымъ, то является слѣдующiй вопросъ: нельзя ли ослабить неудобство, происходящее отъ непрерывной смѣны въ показанiях складывателя, не рискуя результатомъ въ виду выгодъ, представляемыхъ этой непрерывностью для построенiя машины.
Въ машинѣ для сложенiя, которую я имѣлъ честь представить, […] это неудобство почти устранено. Въ окошечкахъ этой машины видны бѣлыя полоски, между которыми легко различить главную, видную во всѣхъ окошечкахъ. Такъ какъ въ первомъ окошечкѣ справа видно только начало этой полоски, то за нею легко прослѣдить, идя справа налѣво. Эта-то полоска и содержитъ всѣ цыфры суммы.
[…]
Разница между истинной величиной переноса и величиной, даваемой эпициклическими механизмами, всегда меньше единицы […]. Слѣдовательно, если сдѣлать окошечки довольно большими, такъ чтобы въ нихъ были видимы одновременно двѣ цыфры барабана, то истинныя цыфры суммы, очевидно, должны быть въ нихъ видны. Что же касается двойственности, представляющейся всякiй разъ, когда въ одномъ и томъ же окошечкѣ видны двѣ различные цыфры, то она легко устраняется благодаря ранѣе упомянутымъ полоскамъ, проведеннымъ на каждомъ барабанѣ, если, кромѣ того, обратить ещё вниманiе на угловыя отклоненiя в положенiи цыфръ слѣдующаго барабана.
Действительно, в разряде единиц лишних смещений у цифрового колеса не бывает — высшие разряды на него действия не оказывают, а справа ничего нет. Значит, цифра единиц всегда стоит чётко по центру, и Чебышева делает окошечко единиц меньше чем все остальные — на одну цифру. Далее нужно, как и указывает автор, двигаться по, в случае первой модели, жёлтым полоскам.
Следуя инструкциям, считываем результат сложения: 415+97=512.
Вслед за Боолем, проведём ещё одно сложение, которое разбирается в его статье: 78352+5467. Действовать нужно точно так же, как и в первом примере. Отметим, что порядок откладывания цифр внутри одного числа значения не имеет — можно начинать с младшего разряда, можно со старшего. Для откладывания любой цифры нужно совершить лишь одно аккуратное действие — взяться за планку ниже нужной цифры на неподвижной шкале соответствующего зубчатого колеса, а потом просто машинально довести эту планку до упора.
Произведём вычитание на арифмометре Чебышева. Рассмотрим пример 76835-4753, разобранный в статье Бооля. Сначала отложим первое число так же, как это делали раньше. Из него надо вычесть 4753. В разряде единиц необходимо взяться за нижнюю планку зубчатого колеса и повернуть его так, чтобы планка оказалась над тройкой. Таким же способом — машинально взяться за нижнюю планку и довести её до положения над соответствующей цифрой неподвижной шкалы. Считывание результата — 72082 — происходит таким же способом, как и при сложении.
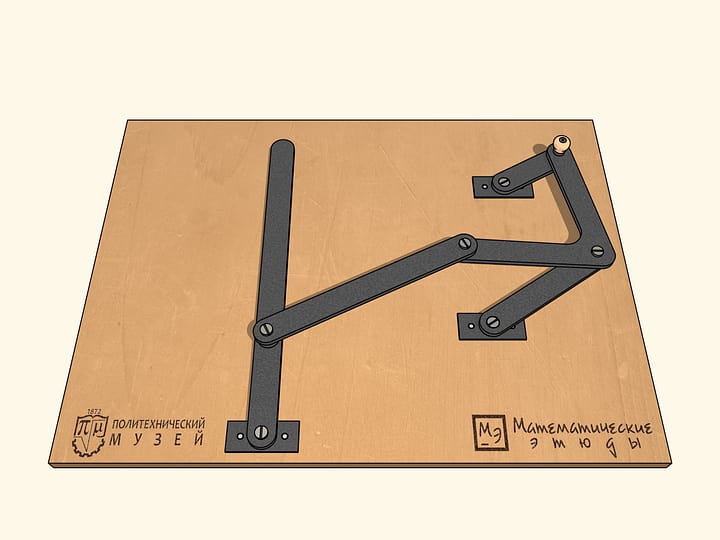
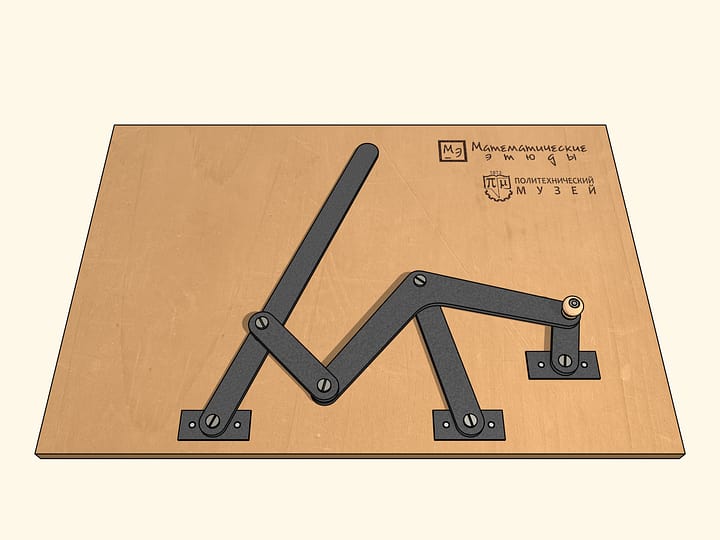
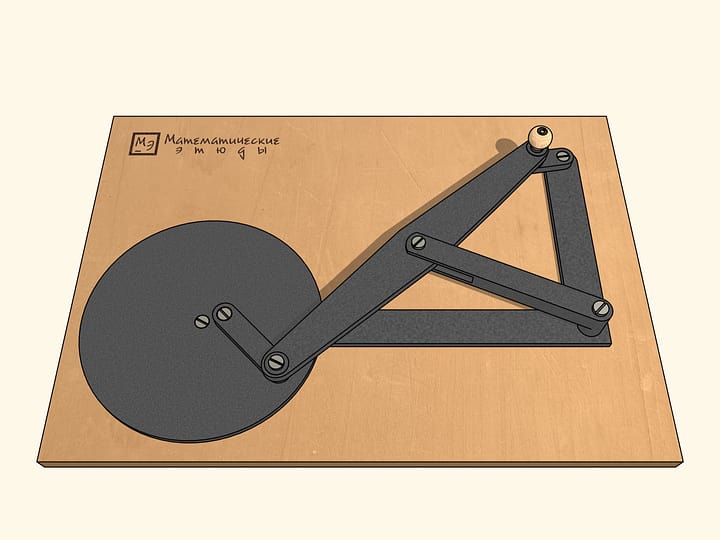
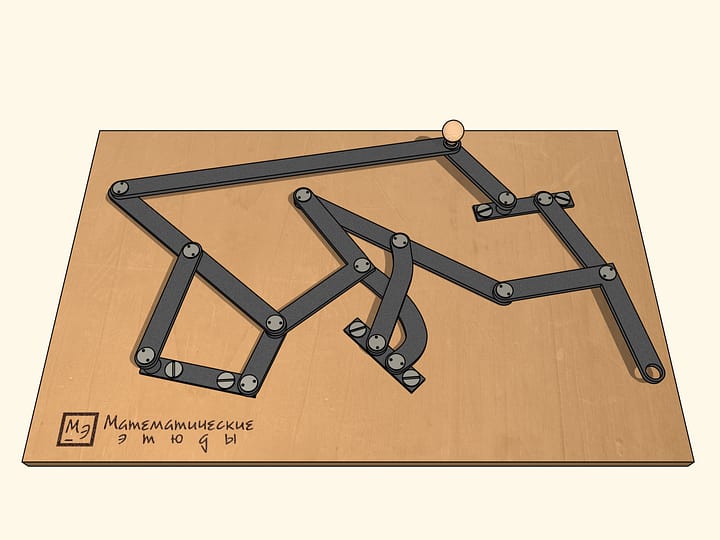
Модель механизма
Геометрическая модель, созданная проектом «Математические этюды».